Shadow of the Knight
Shaodow of the Knight jest to tytuł puzzli na CodinGame.
W skrócie gra ta polega na tym, że wcielasz się w Batmana i szukasz bomby w budynku, którą podłożył Joker.
Jeśli znajdziesz ją, nim ta wybuchnie - uratujesz wszystkich mieszkańców.
Gra podzielona jest na dwa epizody:
Rozwiązanie obu epizodów polega na zastosowaniu algorytmu zwanego binary search. Opiszę rozwiązania obu epizodów, ale wpierw należałoby przytoczyć teorię samego algorytmu i na czym on polega.
Binary search
Binary search - wyszukiwanie binarne - to jeden z podstawowych algorytmów, jaki każdy piszący kod powinien opanować. Polega on na bardzo prostym schemacie. Masz określony zakres i szukasz w nim liczby. Dzielisz zakres na pół i sprawdzasz, w której z tych połówek jest szukana liczba. Tym sposobem, wykluczasz pół zakresu, w jakim szukana liczba się nie znajduje.
Nastepnie wybrany zakres znów dzielisz na pół i znów sprawdzasz, w którym zakresie jest szukana liczba. I tak co turę.
Zakres, gdzie będzie znajdować się szukana liczba zmniejsza się “logarytmicznie”, aż do momentu, gdy znajdziemy szukaną liczbę.
UWAGA!! Zakres liczb, w którym szukamy musi by posortowany.
Prosty przykład: Znajdźmy liczbę \(x = 6\) w zakresie \(n \in [1, 8]\).
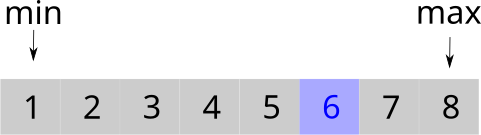
Prostym szukaniem odpytywalibyśmy każdą kolejną liczbę i sprawdzali, czy jest to ta szukana, czyli:
Wykonalibyśmy 6 kroków, by znaleźć liczbę 6. Tym sposobem im zakres by się zwiększał, tym ilość prób by się zwiększała.
To nie jest binary search
binary search - operacja na liczbach

Wykonajmy to samo poprzez binary search.
Wpierw musimy określić nasz zakres, a więc:
\[\begin{align} n_{min} &= 1\\ n_{max} &= 8\\ (n_{min} + n_{max})/2 = 9 / 2 &= 4.5 \Rightarrow \text{zaokrąglamy w górę} = 5 \end{align}\]Zakres dzielimy więc przed liczbą 5.
Powyższe operacje na samych liczbach sprawdzą się, jeśli będą one rosły o 1. W prawdziwych zakresach, w jakich wykonuje się binary search szukamy liczby, jednak niekoniecznie liczby te muszą rosnąć co 1. Mogą mieć różną częstotliwość. Co nie zmieni nam faktu, że indeks na jakim stoi taka liczba będzie rósł o 1, a same liczby muszą być w kolejności następującej po sobie i to rosnąco. Inaczej cały algorytm nie będzie działał, a jeśli cokolwiek znajdzie - to przez czysty przypadek ![]() .
.
binary search - operacja na indeksach
Przypomnę jakie są kolejne indeksy:

Operując na indeksach - bo tak działają algorytmy na zakresach - mielibyśmy:
\[\begin{align} n_{min} &= 0\\ n_{max} &= 7\\ (n_{min} + n_{max})/2 = 7 / 2 &= 3.5 \Rightarrow \text{zaokrąglamy w górę, indeks} = 4 \end{align}\]Na indeksie 4 stoi liczba 5 - wszystko się więc zgadza ![]() . Porównujemy teraz naszą szukaną liczbę
. Porównujemy teraz naszą szukaną liczbę x = 6 do liczby stojącej na środku zakresu w tym przypadku do liczby 5.
- Jeśli jest większa, wybieramy zakres większy i sprawdzamy dalej.
- Jeśli jest mniejsza wybieramy zakres po lewej i sprawdzamy dalej.
- Jeśli jest równa -> BINGO mamy naszą liczbę.
\(n_{mid}+1\) ponieważ w tym miejscu zaczyna się dzielony zakres.
\[\begin{align} \text{1) ---------- Runda 2 ----------} \\\\ (n_{min} \text{, } n_{max}) & = (5, 7)_{indeksy} \\ n_{mid} &= (n_{min} + n_{max})/2 \Rightarrow (5+7)/2 = 6\\\\ (n_{min} \text{, }n_{mid}, n_{max}) & = (5, 6, 7)_{indeksy} = (6, 7, 8)_{liczby} \\\\ 6=n[n_{mid}] \Rightarrow 6=n_{6} \Rightarrow 6=7 &\Rightarrow {NIE } \\ 6<n[n_{mid}] \Rightarrow 6<n_{6} \Rightarrow 6<7 &\Rightarrow {TAK } \rightarrow \text{wybieramy mniejszy zakres}\\ 6>n[n_{mid}] \Rightarrow 6>n_{6} \Rightarrow 6>7 &\Rightarrow {NIE }\\ (n_{min}, n_{max}) &= (n_{mid}, n_{max}-1) = (5, 5)_{indeksy}\\\\ \text{1) ---------- Runda 3 ----------} \\\\ (n_{min} \text{, } n_{max}) & = (5, 5) \\ n_{mid} &= (n_{min} + n_{max})/2 \Rightarrow (5+7)/2 = 6\\\\ (n_{min} \text{, }n_{mid}, n_{max}) & = (5, 5, 5)_{indeksy} = (6, 6, 6)_{liczby} \\\\ 6=n[n_{mid}] \Rightarrow 6=n_{5} \Rightarrow 6=6 &\Rightarrow {TAK } \rightarrow \text{KONIEC ALGORYTMU}\\ 6<n[n_{mid}] \Rightarrow 6<n_{5} \Rightarrow 6<6 &\Rightarrow {NIE }\\ 6>n[n_{mid}] \Rightarrow 6>n_{5} \Rightarrow 6>6 &\Rightarrow {NIE }\\ \end{align}\]Liczbę 6 w zakresie od [1, 8] znaleźliśmy w 3 krokach.
Przekształćmy to na kod:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
collection = [1,2,3,4,5,6,7,8] # 8 elementów
i = 1
def binary_search(i, collection, item):
print("Szukana liczba:", item, "\n")
print("Zakres:", collection, "\n")
start = 0
stop = len(collection) - 1
while start <= stop:
middle = round((start + stop)/2)
#middle = (start + stop)>>1
guess = collection[middle]
# ten fragment tylko wypisuje kolejne kroki, nie należy on do samego algorytmu
print("---runda {}---\nzakres: {}\nnmin: {} -> liczba: {}
\nnmax: {} -> liczba: {}\nśrodek: {} -> szukana liczba?: {}\n".format(
i, [*(i for i in collection[(start):(stop+1)])],
start,collection[start],
stop, collection[stop],
middle,guess))
# tutaj zaczyna się sam algorytm
if guess == item:
return middle
if guess > item:
stop = middle - 1
else:
start = middle + 1
i += 1
return False
x = 6
index = binary_search(i,collection, x)
print("Szukana liczba: {} jest na indeksie:
{}".format(x, collection[index]) if index else 'Brak dopasowania')
A działa on tak:
Jak wcześniej wspomniałam, zakres liczb musi być posortowany inaczej binary search zawiedzie:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Szukana liczba: 6
Zakres: [1, 2, 5, 8, 7, 6, 4, 3]
---runda 1---
zakres: [1, 2, 5, 8, 7, 6, 4, 3]
nmin: 0 -> liczba: 1
nmax: 7 -> liczba: 3
środek: 4 -> szukana liczba?: 7
---runda 2---
zakres: [1, 2, 5, 8]
nmin: 0 -> liczba: 1
nmax: 3 -> liczba: 8
środek: 2 -> szukana liczba?: 5
---runda 3---
zakres: [8]
nmin: 3 -> liczba: 8
nmax: 3 -> liczba: 8
środek: 3 -> szukana liczba?: 8
Brak dopasowania
Wiedząc już jak działa binary search możesz spróbować rozwiązać Epizod 1 - Shadow of the Knight. Opiszę go w swoim następnym wpisie ![]()
